KNDY

○点透視図法

最終更新：2014年09月04日 15:58

匿名ユーザー

- view

管理者のみ編集可

このページでは一～三点透視図法について考察してみよう。それぞれの図法ごとにページを分けなかったのは、それぞれの関係を明らかにしつつ一気にやってしまった方がいいと思ったからだ。長くなるので以下に目次。

○点透視図法とはそもそも何ぞ
視線と○点透視図法
一点透視図の消失点
二点透視図の消失点
三点透視図の消失点

○点透視図法とはそもそも何ぞ

○点透視図法は透視図法により、直交座標系を描く方法のことである。少なくとも筆者はそう理解している。そうそう、普段お世話になるwikipediaだが、遠近法関連の項目は当分の間は読まないことにした。本稿より優れて明確な説明を見るだけでモチベーションが低下すること請け合いであろうから。閑話休題(使ってみたかっただけだ)。で、その直交座標系とは何のことを云っているのか。簡単に言えば整然と並んだ直方体のみで構成されるような世界である。つまり、高さ・幅・奥行きを表す3方向の直線のみで構成された世界、といえる(別に斜めの線や曲線があっても構わないのだが、それらの基準として直交する3軸を用いるのだ。)。たとえば建物や家具などは基本的にこの3方向の直線で構成されているので、この直交座標系を遠近法で描くことが出来れば、基本的な風景はそれっぽく描くことが出来るのではなかろうか、と考える次第であります(語尾を濁す)。

ところで○点透視図法の○点とは何の点がいくつだと云うのであろう。1点から3点までしかないのは、描く対称が直交座標系であり直線の方向が3方向に限定されるからである。では点は何の点だというのやら。それはかの有名な消失点のことである。「地面の極限として画面上に水平線が現れ」たように、「直線の極限として画面上には消失点が現れる」のである。そして(たとえ画面上に現れなくとも作図にあたって考慮すべき)消失点の数が、直交座標系と視線との位置関係変わってくるため、一～三点透視図法が存在するのだ。

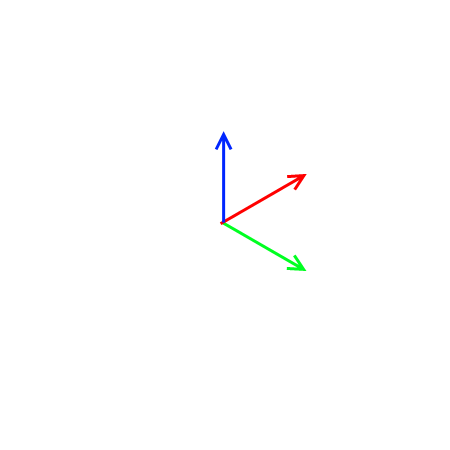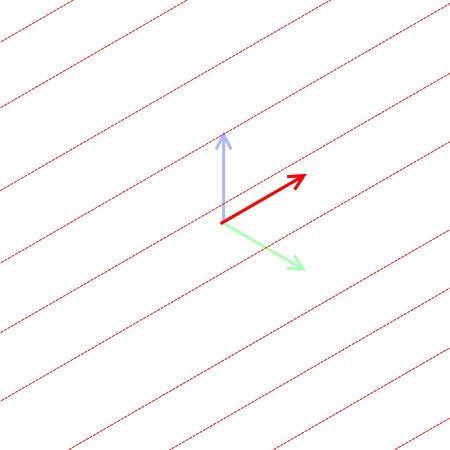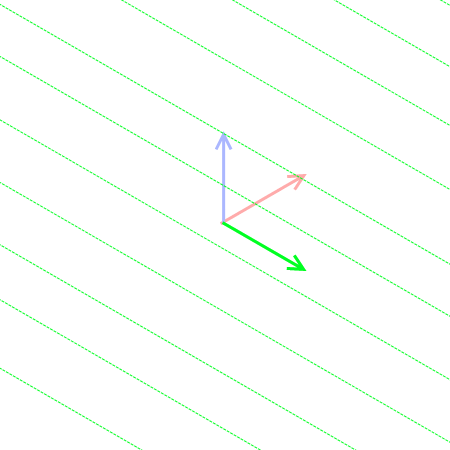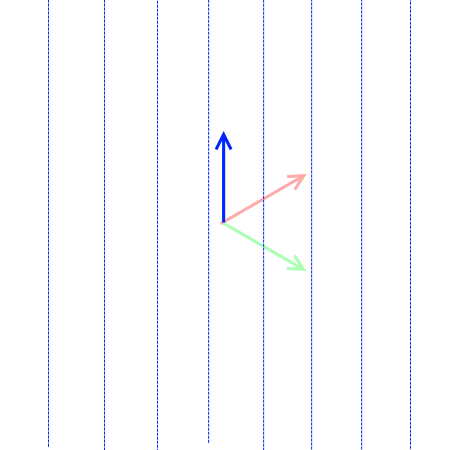
視線と○点透視図法

○点透視図法において、けだし最も重要な法則、それは｢視線方向に対し垂直な方向を持つ平行線群は消失点を作らない｣、あるいは｢視線方向に対し垂直でない方向を持つ平行線群は必ず消失点を作る｣ということであろう。平行線群というのは上の図からイメージしてもらいたい。このことを踏まえ、一～三点透視図法における直交座標系と視線の関係を簡単に見てみよう。

一点透視図法: 互いに垂直な三軸のうち、二軸が視線に垂直な方向を持っている場合、この二軸方向の直線は消失点をつくらないので、消失点を作るのは残りの一軸方向のみとなる。これが一点透視。
二点透視図法: 今度は三軸のうち一軸のみが視線に垂直な場合である。残りの二軸方向の直線が消失点を作るため、二点透視となる。
三点透視図法: いちいち説明するまでもなく、三軸全てが視線方向に垂直ではない場合であり、消失点は三つになる。

というわけで、これから消失点と画面の中心点(視線の延長)との厳密な位置関係について考察していくことにする。

▲上へ

一点透視図の消失点

先ほど述べたように、一点透視の場合二軸は視線に垂直である。すると、残りの一軸は自ずと視線に平行な向きになることが分かる。

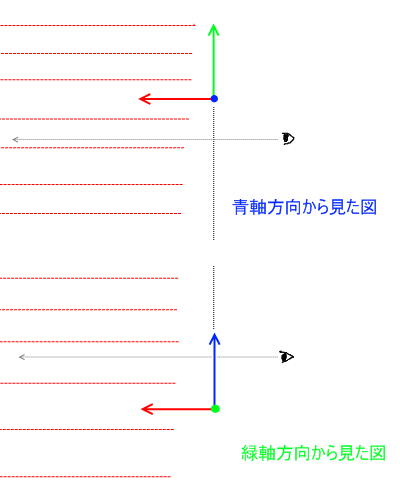
そして、上の図でいう赤軸方向の直線は、水平線の時と同様に考えると、視線の極限である画面の中心点に点を結ぶことが分かる。

つまり、｢一点透視図法における消失点は必ず画面の中心点(あるいは鑑賞者の目線を誘導したい点)になる｣と云うことが出来る。

あれ？今回はひょっとして三角関数なし？

▲上へ

二点透視図の消失点

続いては二点透視だ。分かりやすいように青軸を地面に垂直に保ったまま、赤軸と緑軸を角度 $\alpha$ だけ回転させた場合を考えよう(角度のハナシが出てきた時点で嫌な予感を感じてよい)。もちろん、どの方向の直線ががどっちを向いていようが、作図の後で画面を回転させれば同じことなので、大事なのは視線に対する軸の角度だ。

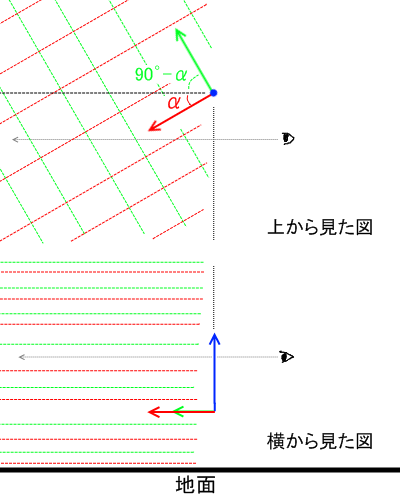
横(便宜上そう呼ぶ)から見た図でわかるように、地面に平行である赤・緑軸方向の直線群は、どうやら水平線上で点を結ぶようである。さらに上から見ると(アオリ・フカンのときの議論を踏まえ)赤線は $\alpha$ 、緑線は $(90^\circ -\alpha)$ 方向に点を結ぶようだ。
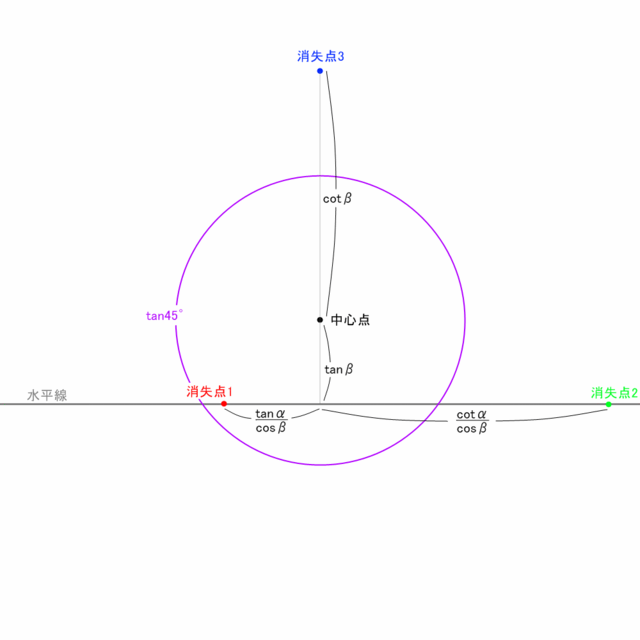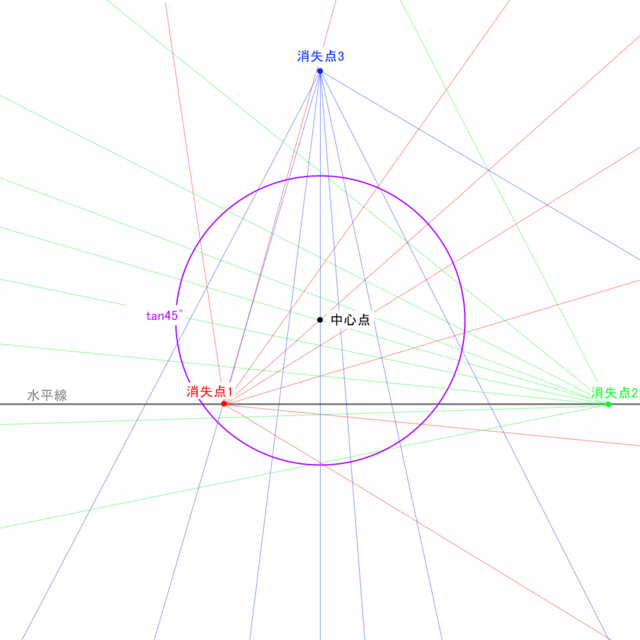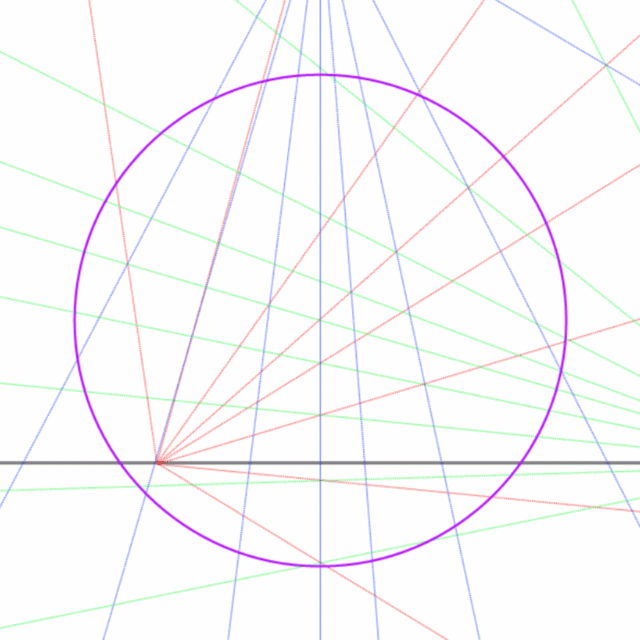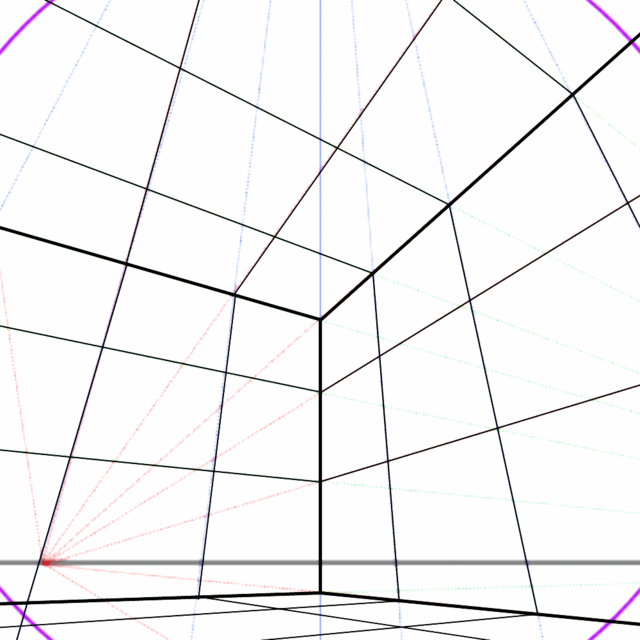
よって赤・緑軸方向の消失点は上画面の中心点から、水平線に沿って $\tan\alpha$ および $\tan(90^\circ -\alpha)$ の位置に現れる(やっぱり出てきちゃったねタンジェント)。ちなみに $\cot\alpha=\tan(90^\circ -\alpha)=\frac{1}{\tan\alpha}$ という便利な関数も存在する。嘘みたいだがコタンジェントと読む(パンダコパンダみたいなものであろう*1)。つまり下の図でいう消失点1～中心点間の距離と中心点～消失点2間の距離の比は $\tan\alpha : \cot\alpha$ となる。

もちろん話はこれだけではない。中心点と消失点の位置関係がわかったら、今度は画面のサイズを適切に決めなければならない。人間が視認できる範囲は視線に対しおよそ45°程度といわれているので、画面上で中心点から $\tan45^\circ$ 以上離れた位置は不自然にゆがんで見えることになる。上の図には半径比 $\tan45^\circ$ の円を描き入れたが、感覚的に自然な構図にしたければ、画面はこの円よりも小さくてしかるべきである。
ところで、これは何も二点透視図法に限られたことでありませんが、｢きちんと消失点を意識して構図をつくったのに、出来た画面の遠近感が何故か不自然！｣そんなあなた!! すなわちそれは少なくとも以下のどちらか一方が原因です。

透視図法の中心点が構図の中心(あるいは主題の位置)からずれている
画面に描かれた範囲が広すぎる(画角が大きすぎる)

例えば、もし上の図のようにひとつの画面の中にに消失点が2つ以上描かれていたら、それは明らかに画角が大きすぎである。
この $\tan45^\circ$ はひとつの目安となる(=1なので扱いやすい)ため、以降もちょくちょく顔を出すと思う。そのつもりで。

▲上へ

三点透視図の消失点

ようやく、ついに、ここまでやって来た。上の二点透視の説明で用いた図をもとにして、今度は下の図のような場合を考える。

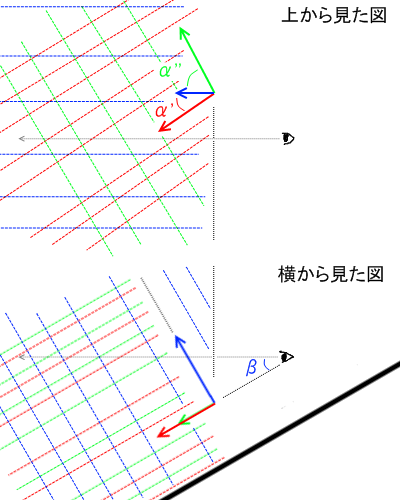
先ほどと同じく、青軸は地面に垂直に保ったまま赤軸を本来の位置から角度 $\alpha$ だけ回転させているのだが、今度は視線を $\beta$ 上に傾けることにする。(視線を基準としているので、上の図では軸の方が $\beta$ 下に傾いたように描かれている。)すると、これまでの説明から分かるように(分かる･･･よね･･･？)水平線は画面中心点から $\tan\beta$ 下の位置に、青軸方向の直線の消失点は $\cot\beta$ 上の位置に現れる。また、今度は視線と地面が水平でなくなるため、｢上から見た図｣における $\alpha '$ は $\alpha$ よりも大きな角度に見え、また赤軸と緑軸も直交していないように見えるため、 $(90^\circ -\alpha)$ はより大きい角度 $\alpha ''$ に見えることになる。この図から、水平線の中心から $\tan\alpha '$ の位置に赤軸の消失点が、 $\tan\alpha ''$ の位置に緑軸の消失点が現れることが想像していただけるであろう。詳しい説明は割愛させていただくが、この $\alpha ' ,\alpha ''$ については $\tan\alpha ' = \frac{\tan\alpha}{\cos\beta}$ , $\tan\alpha '' = \frac{\cot\alpha}{\cos\beta}$ という関係がある。これはもう、こういうものだと思って貰えればいい。
とにもかくにも、これで画面上の3つの消失点の位置を決めることが出来たわけだ。あとは、画角を適当に調整するだけだ。

ね？簡単でしょ？

｢全然。もっと簡単に出来ねーのかよ？｣

▲上へ

（最終更新日：2014年09月04日）

&link_trackback(text=トラックバック表示)

もうちょっと簡単に描く描き方を教えてください -- 名無しさん (2011-06-18 10:57:04)
なるほど、わからん -- 名無しさん (2011-07-21 18:08:33)
応用の仕方を詳しく教えて下さると助かります -- 名無しさん (2011-08-12 21:48:05)
分かりやすかったです！＿視円錐と消失点の関係をもう少し説明してください。 -- 毛無しさん (2014-09-04 15:58:00)

タグ：

遠近法考察

「○点透視図法」をウィキ内検索

添付ファイル